【すぐわかる！】粉体の流動性とは

こんにちは。

群馬県高崎市の表面処理業者、株式会社三和鍍金と申します。

本コラムは事業統括部の柳沢が解説いたします。

今回は粉体の流動性についてのコラムになります。

弊社では粉体を使った塗装「粉体塗装」を承っておりますのでお気軽にお問合せ下さい

それはなんですか、という方がほとんどでしょう。

弊社でも扱っている粉体塗装という工業塗装では、塗料を粉末化した「粉体塗料」を用いて塗装を行いますが、

この粉体の流動性という性質が、実は良質な粉体塗装には欠かせないエッセンスなのです。

粉体の流動性とは何なのか

解説していきたいと思います。

粉体塗装とは

まずはじめに、粉体塗装について軽くご説明いたします。

粉体塗装とは工業塗装の一種で、前述した通り粉末化した塗料である「粉体」を用いて塗装を行います。

別名パウダーコーティングとも呼ばれます。

耐食性や耐候性に優れるため様々な場所に採用され、皆さんの周りにもありふれている塗装と言えるでしょう。

溶剤を用いないため、人と環境にやさしい塗装として近年注目を集めています。

その他詳しくはこちらのリンクからご覧いただけます。

また、弊社でも粉体塗装は取り扱っておりますので、対応可能寸法などはこちらからご参照ください。

粉体の流動性とは

流動性という言葉自体は、モノが流れ動く容易さ全般を表しています。

これはたとえば経済学などでも用いられるように、観念的な部分をも含んでいます。

ただ、今回お話する粉体の流動性はもっとシンプルで、実際は皆さんも体験したことのあるような事象を学問的に表しているだけなのです。

砂時計の例

皆さんは、砂時計を手に取ったことはありますか。

特徴的な形の瓶の中に砂が入っていて、瓶の片側から片側へ砂が落下する時間をタイマーとして使うことが出来るもの。

私がはじめて砂時計を目の前にしたときは、好奇心でひたすら砂が落ちていくところを眺めていたものです。

そうすると、あることに気づきます。

かさが増えていくとき、砂は液体のように平らなまま増えていきません。

落ちていき底に着いたあと、砂は最初こそ液体のように平らですが、だんだんと山のように中央が隆起した形に変わっていきます。

そして一定の形まで盛り上がったあとは、その形のままかさがどんどんと増えていくのです。

現象としてはなんてことのない、誰しも経験のある事象ですが、ここに粉体の流動性の話が隠れています。

キーワードとしては2つ、

「安息角」と

「かさ比重」です。

それぞれどのような意味なのでしょうか。

安息角とは

まずは恒例のワードの分解をしてみましょう。

安息＝落ち着いている

角＝角度

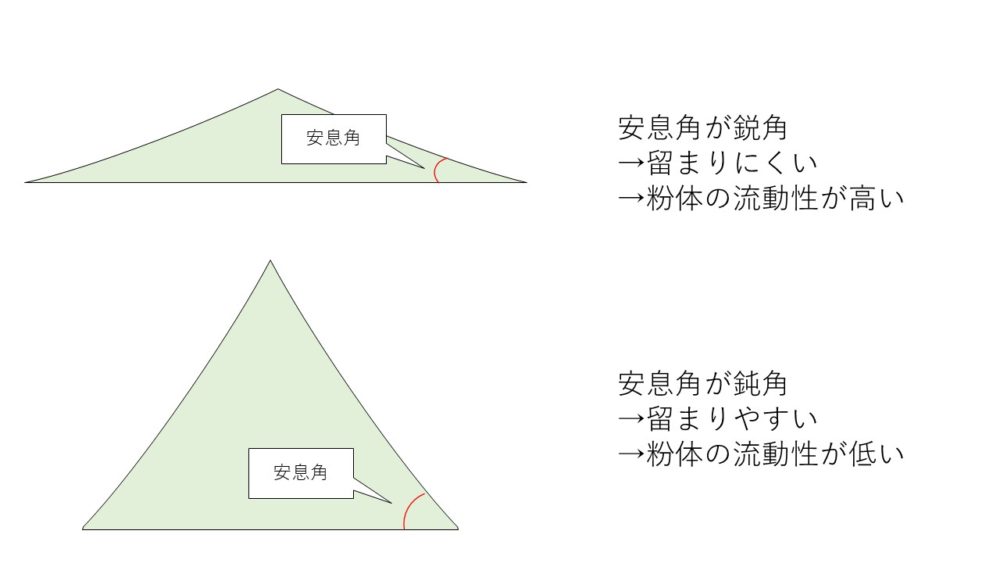
砂時計でいえば「砂が落ち着く角度」のことを「安息角」と言います。

どういうことか。

先ほどお話した通り、砂など粉末状のものを上からサラサラと平面に落とすと、だんだんと盛り上がってきますよね。

重要なのはそのあとで、いつまでも盛り上がり続け、最終的には針のように細く高く積もる・・・なんてことはないはずです。

ある程度の斜面角度をもつ山になれば、それより急な斜面にはならないのです。

この時の水平面と山の斜面との角度を、その物質の「安息角」と呼びます。

粉体であれば、安息角が鈍角であればあるほど例えば水分を含んでいて重たいような感じで

安息角が鋭角であれば、それだけサラサラとしているイメージです。

私は雪国育ちなので、あまり寒くない日に降る少し溶けているような固まりやすい雪と、

とても寒い日に降るサラサラの、いわゆるパウダースノーを思い浮かべると腑に落ちます。

そして、どちらが流動しやすいかと言われれば、皆さんお分かりの通り、サラサラの方ですよね。

したがって、「安息角が小さくなる粉体は流動性が高い」と言えるわけです。

逆に、「安息角が大きくなる粉体は流動性が低い」、とも。

かさ比重（嵩比重）とは

もうひとつのキーワードは「かさ比重」です。

「比重」と聞くと途端に難しくなった気がしますが、そんなことは決してありません。

水と「比」べた「重」さのことですから。

なぜ「水」かというと、水はほぼ1ml＝1gであるため比較するのに都合がいいというわけです。

たとえば比重が1.1の液体物質Aがあったとすれば、同じ500mlでも水は500g、物質Aは510gとなるということです。

液体として同じ量なのに重さが違うというのはなんだか不思議な気がしますが、これが最もシンプルな比重の例になります。

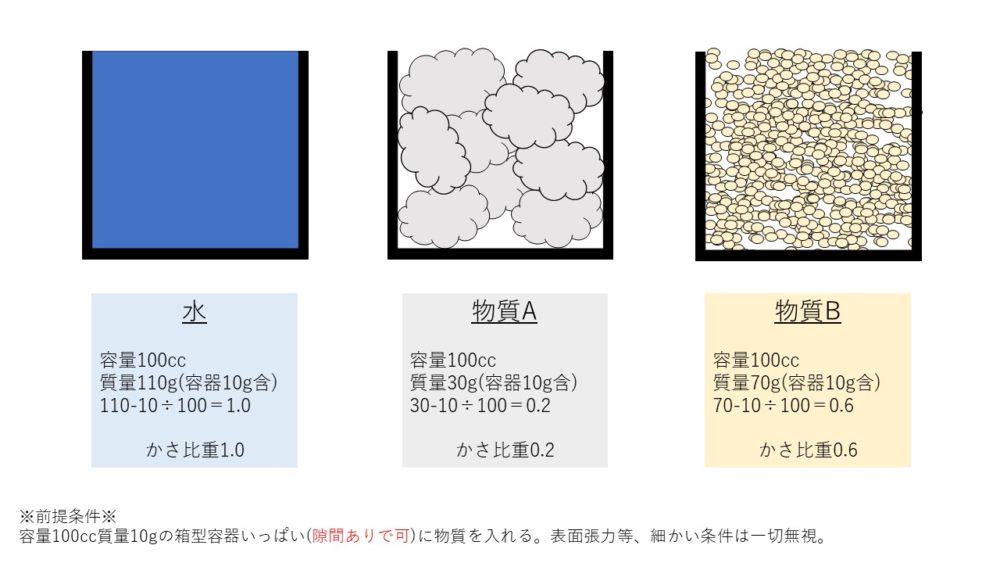
そして、物質がある容積を満たすときの質量をその容積で割ったものを「かさ比重」と言います。

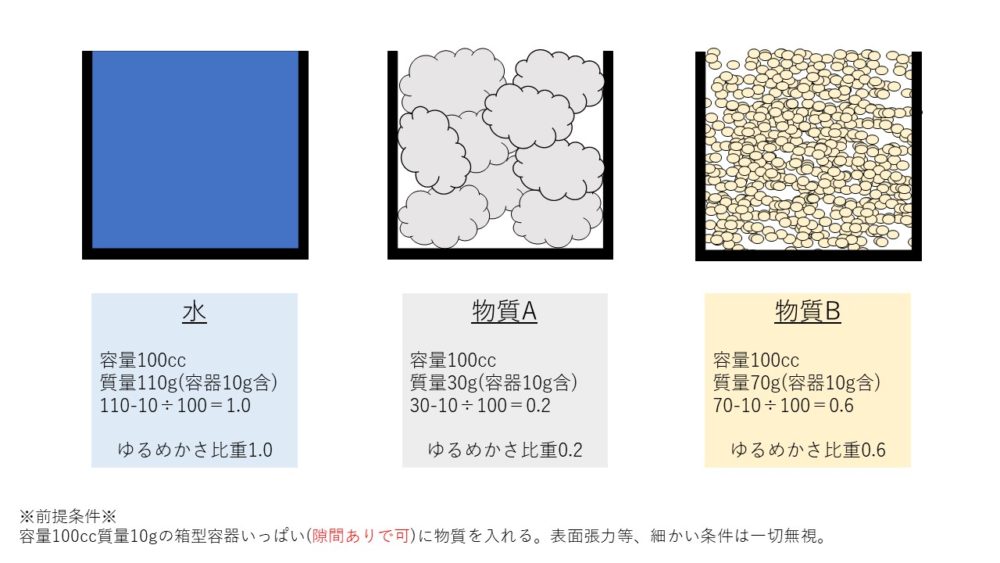
仮に下図のように水、物質A、物質Bのかさ比重を求めた場合は、以下のようになります。

水　1.0　

物質A　0.2

物質B　0.6

ここで重要なのは、たとえば物質Aが綿だったとして、ギュッと力を込めて箱に入れればたくさん入るということです。

したがって、容器にあまり力を加えずゆるめに入れた場合（ゆるめかさ比重）とぐっと力を入れて押し込んだ場合（きつめかさ比重）で

質量もといかさ比重は変化してくることがお分かりになるかと思います。

上の例をゆるめだと仮定し、それぞれきつめにした場合には倍以上入るとすると、

それぞれのきつめかさ比重は以下のようになります。

水　1.0　※押し込むという概念がないため、きつめでも等倍

物質A　0.8　※ゆるめ時のおよそ4倍入る仮定

物質B　1.3　※ゆるめ時のおよそ2倍入る仮定

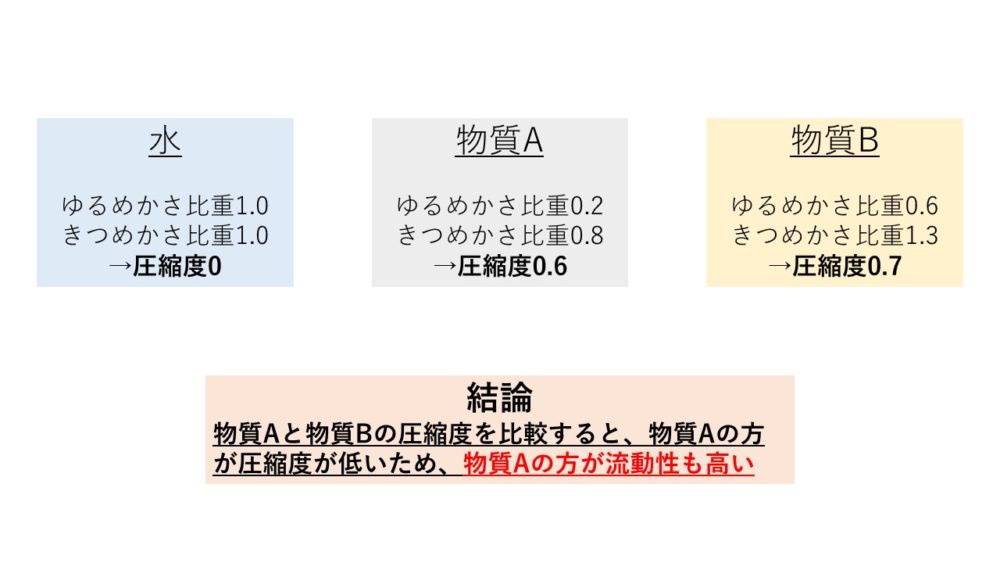
このゆるめかさ比重ときつめかさ比重の差が、物質Aと物質Bで異なることがお分かりかと思います。

物質Aはその差0.6、物質Ｂはその差0.7、さらに言えば、水は差が0です。

遠回りしてしまいましたが、この差の大きさが流動性を考える上で重要な指標になってくるのです。

差が小さければ小さいほど流動性が高く、大きければ大きいほど流動性は低いと言えます。

また、この「差」は「圧縮度」あるいは「圧縮性」と呼ばれています。

水は非常に流動的ですよね。したがって、「差が0（圧縮性がなく）であり流動性が高い」のです。

このように物質Aと物質Bの流動性をかさ比重（圧縮度）を基準にして考えると、

物質Aの方が若干ながら流動性が高い物質である、と証明ができます。

こんな感じで理論的にかさ比重を説明してきましたが、もっと感覚的に理解するため

例えば先ほどの雪の話に戻ってみましょう。

パウダースノーは前述した通りサラサラしているので固まりにくいです。

雪合戦をするならどちらかというと牡丹雪のようなもっともったりとした雪の方が固まりやすさから適しています(余談)。

固める＝圧力をかけて縮める＝圧縮することなので、固まりにくいということはすなわち圧縮性が低い、

つまり流動的であると言えるのです。

ではどのように圧縮性を求めるかというと、計算上でギュッとしてみれば良い・・・ということで

前述したかさ比重の計算、ゆるめときつめの比較が出てくるわけですね。

粉体の流動性と粉体塗装の関係性

粉体の流動性についてはご理解いただけたかと思います。

では、粉体の流動性と粉体塗装にはどのような関係性があるのでしょうか。

リード文でちらっと触れた通り、粉体塗装において粉体塗料の流動性は非常に重要です。

小麦粉のような固まりやすい粉体ですと、均一な塗膜形成が難しく不具合につながってしまいます。

逆にサラサラであれば流動性が良いため細部にまで均一に届き、高品質な塗装が可能となるのです。

当社では流動性の高い粉体を用いた粉体塗装を扱っておりますので、お客様に美しい塗装をご提供が可能となっております。

当社粉体塗装についてはこちらのリンクから詳細がご覧いただけます。

蛇足～密度と比重～

既に少し書きすぎている本コラムですが、恒例の蛇足を最後に加えさせてください。

今回は密度と比重についてです。

恐らく中学校の理科などで習った内容だと思うのですが、私はすっかり忘れておりよくわかっておりませんでした。

今回のコラムを書くにあたって密度という言葉すらないものの、知識として間違いなく必要であったことですので

併せてご紹介したいと思います。

コラムを書いている途中、様々な文献を参照しながら「かさ比重」について学んでいた際に

「質量を容積で割る」という言葉を見つけ、私は思いました。

それ、密度じゃん？？？

密度＝質量÷体積

ということは密度＝かさ比重なのか・・・？

そこでたどり着いた結論が「水の密度は1」ということです。

前述した通り水は1mlが1gになります。

1ml＝1㎤になるので、水は1ml＝1㎤＝1gになるわけです。

ここで、1㎤あたりの水の密度を求めてみましょう。

密度の公式は上に載せました。

そうです、全てが1になるため、計算せずとも答えが1g/㎤であることは明白ですね。

さて、実は先の段落で「比重」の定義をあえて曖昧にした私ですが、

ここで改めて「比重」について考えてみます。

比重とはあるモノの密度を水の密度で割った数値になります。

あるモノの密度を〇とし、水の密度を□としてみましょう。

そうすると、比重＝〇/□になりますね。このとき、□は変数ではないのです。

そう、1ですね。

したがって分母が必ず1になるので、結果的に数値としては比重＝〇＝密度となるというわけです。

重要なのは意味として同じではないということ。

あくまでも比重はある物質の密度と水の密度の対比により決定するものだからです。

※厳密にいえば、水は温度によってその体積が変わります。この理論に最も当てはまるのは4℃のときです。

さて、では最初に戻って本当に密度＝かさ比重なのかを考えてみます。

先に出した物質Aを例にとってみます。

計算式によって出てきた0.2という数字は100ccという限定された体積で物質Aの質量を割った、

あくまでも「密度」です。

※この密度は「かさ密度」と呼ばれます。かさとして限定された体積で割っているためです。

この密度を水の密度1で割り、水の密度と対比した「0.2」という数字、

これこそが「かさ比重」なのです。

「密度」と「かさ比重」は、あくまでも数値が一緒というだけなのです。

いかがだったでしょうか。

少しでもわかりやすいと思っていただけたら幸いです。

では、また次回のコラムにて。